Dans le répertoire javascript créez un dossier cours9. Il contiendra tous les fichiers de cette
leçon.
Sur l'éditeur Brackets allez dans Fichier, ouvrez un dossier et sélestionner le dossier cours9.
Le nom du dossier s'affiche à gauche.
A l'aide d'un clic droit de la souris sur le nom du dossier,
créez un dossier js puis un dossier html.
1. Définition
Un matrice est représentée en javascript par une liste de listes.
Exemple : matrice=[[1,2,3],[4,5,6],[7,8,9]] équivaut à :
$\left( \begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array}\right). $
C'est une matrice 3 lignes, 3 colonnes.
Ainsi pour désigner l'élément 1 de la matrice situé en première ligne, première colonne,
nous utiliserons les indices (0,0), soit matrice[0][0].
matrice[0] désigne la liste [1,2,3] et matrice[0][0] le premier élément de cette liste.
De même matrice[1][2] désigne l'élément de la matrice situé
à la ligne 2, colonne 3 soit 6.
Exercice 1 : création d'une matrice.
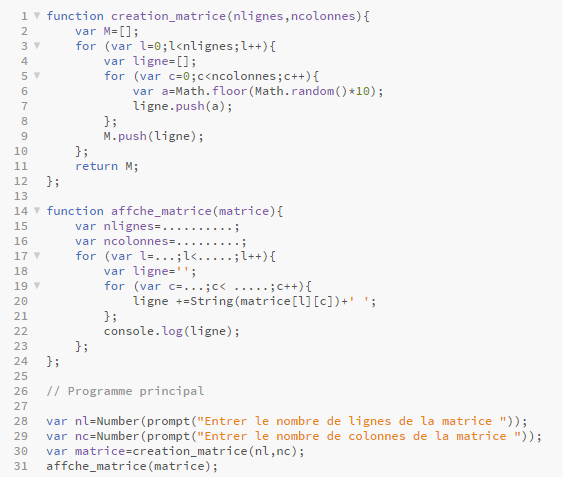
Ecrivez le script javascript creation_matrice.js ci_dessous :

En ligne 2 nous créons M une liste vide.
Nous avons une double boucle. La première en ligne 3 génère les lignes et la deuxième en ligne 5, les colonnes.
La ligne est complétée en ligne 6 et 7.
Une fois la ligne finie, on l'ajoute à la liste M en ligne 9, puis on la "vide" en ligne 4 pour
constituer la ligne suivante.
Exercice 2 : affiche d'une matrice.
Complétez le script javascript affiche_matrice.js ci-dessous qui affiche la matrice ligne par ligne comme ceci : $\begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array} $
Exercice 3 : somme de deux matrices.
Ecrivez le script javascript sommes_matrices.js qui fait la somme de deux matrices :
$$\quad\left( \begin{array}{ccc}1&2&3\\4&5&6\\7&8&9
\end{array}\right) \quad + \quad \left( \begin{array}{ccc}10&11&12\\13&14&15\\16&17&18
\end{array}\right) \quad = \quad \left( \begin{array}{ccc}11&13&15\\17&19&21\\23&25&27
\end{array}\right) $$
Ce script contiendra les fonctions creation_matrice(nlignes,ncolonnes), affiche_matrice(matrice)
écrites précédemment et vous rajouterez la fonction somme_matrices(matrice1,matrice2).
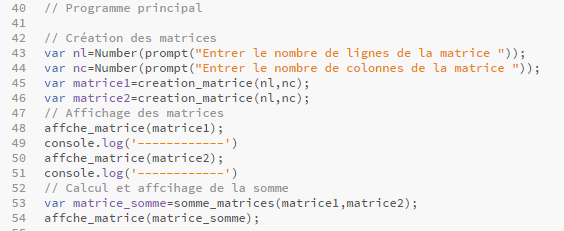
Le programme principal du script est donné ci-dessous :
Exercice 4 : sommes des lignes.
Ecrivez le script javascript sommes_lignes_matrice.js qui calcule la somme de chaque ligne d'une matrice:
$\left( \begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array}\right) $ donne [6,15,24]
Ce script utilisera les fonctions creation_matrice(nlignes,ncolonnes), affiche_matrice(mat)
précédentes puis la fonction somme_lignes_matrice(matrice) qui retournera la liste sommes
Exercice 5 : sommes des colonnes.
Ecrivez le script javascript sommes_colonnes_matrice.js qui calcule la somme de chaque colonne d'une matrice: $\left( \begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array}\right) $ donne [12,15,18]
Exercice 6 : sommes des diagonales.
Ecrivez le script python sommes_diagonales_matrice.js qui calcule la somme de chaque diagonale d'une matrice carrée: $\left( \begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array}\right) $ donne [15,15]
2. Création d'une matrice du sudoku
Le but de ce travail consiste à créer une matrice carrée de taille t composée d'entiers compris dans l'intervalle $\left[1; t^2\right] $. Tous ces entiers doivent être différents et disposés dans la matrice de manière aléatoire. Pour cela vous devez créer quatre fonctions :
- la fonction affiche_matrice(matrice) qui permet d'afficher la matrice de taille $t$
- la fonction liste_ordonnee(taille) qui permet de créer une liste L ordonnée d'entiers allant de 1 à $t^2$
- la fonction liste_desordonnee(L) qui mélange les entiers contenus dans L. Aide : Algorithme
- la fonction matrice_nombres(L) qui permet de créer la matrice des entiers contenus dans la liste L où les entiers ont été mélangés. Aide : Algorithme
On donne le programme principal :

3. Le carré magique
En mathématiques, un carré magique d’ordre n est composé de $n^2$ entiers strictement positifs, 1,2,3 .....$n^2$, écrits sous la forme
d’un tableau carré.
Ces nombres sont disposés de sorte que leurs sommes sur chaque rangée, sur chaque colonne et sur chaque diagonale principale soient égales.
On nomme alors constante magique (et parfois densité) la valeur de ces sommes.
Cette constante magique est égale à $ \dfrac{n\left(n+1 \right) ^2}{2}$.
Exemple :
Carré magique d'ordre 3 : $$\begin{array}{|c|c|c|}
\hline
8&1&6\\
\hline
3&5&7\\
\hline
4&9&2\\
\hline
\end{array}.$$
Constante magique :$ \dfrac{3\times 4^2}{2}=15$.
On souhaite construit des carrés magiques d'ordre impair.
Pour cela on pourra utiliser la méthode suivante :
- Placez un 1 au milieu de la première ligne
- Après avoir placé $k$ dans le carré en $(i,j)$ , placez $k+1$ dans le carré à droite et vers le haut,
soit en $(i+1,j+1)$ en défilant au-delà des bordures, c'est à dire que si la case dépasse la première ligne
(resp. la dernière colonne), la case sélectionnée est celle en dernière ligne (resp. en première colonne).
En cas d'occupation d'une case, la case suivante est recalculée sous la case courante.
Explication pour un carré d'ordre 3 :
Étape 1 : $\begin{array}{|c|c|c|}\hline
.&1&.\\\hline .&.&.\\\hline .&.&.\\\hline
\end{array}$
.
Étape 2 : $ \begin{array}{cccc}
\begin{array}{ccc}
~&~&(2)\end{array}\\
\begin{array}{|c|c|c|}\hline
.&1&.\\\hline .&.&.\\\hline .&.&.\\\hline
\end{array}&\Longrightarrow&
\begin{array}{|c|c|c|}\hline
.&1&.\\\hline .&.&.\\\hline .&.&2\\\hline
\end{array}&
\text{ On dépasse la première ligne, on met 2 à la dernière ligne.}
\end{array}$
.
Étape 3 : $ \begin{array}{ccccc}
\begin{array}{|c|c|c|}\hline
.&1&.\\\hline .&.&.\\\hline .&.&2\\\hline
\end{array}&
\hspace{-0.4cm}\begin{array}{c}
\\(3)\\\\
\end{array}
&\Longrightarrow&
\begin{array}{|c|c|c|}\hline
.&1&.\\\hline 3&.&.\\\hline .&.&2\\\hline
\end{array}&
\text{ On dépasse la troisième colonne , on met 3 à la première colonne.}
\end{array}$
.
Étape 4 : $ \begin{array}{ccccc}
\begin{array}{|c|c|c|}\hline
.&1&.\\\hline 3&.&.\\\hline .&.&2\\\hline
\end{array}&
\begin{array}{|c|c|c|}\hline
.&1&.\\\hline 3&.&.\\\hline 4&.&2\\\hline
\end{array}&
\text{La case est occupée par 1 on met 4 en dessous de la case courante.}
\end{array}$
.
Étape 5 :
$\begin{array}{|c|c|c|}\hline
.&1&.\\\hline 3&5&.\\\hline 4&.&2\\\hline
\end{array}$
.
Étape 6 :
$\begin{array}{|c|c|c|}\hline
.&1&6\\\hline 3&5&.\\\hline 4&.&2\\\hline
\end{array}$
.
Étape 7 :
$ \begin{array}{ccc}
\begin{array}{cccc}
~&~~~&~~~&~~~(7)\end{array}\\
\begin{array}{|c|c|c|}\hline
.&1&6\\\hline 3&5&.\\\hline 4&.&2\\\hline
\end{array}&\Longrightarrow&
\begin{array}{|c|c|c|}\hline
.&1&6\\\hline 3&5&7\\\hline 4&.&2\\\hline
\end{array}
\end{array}$.
On dépasse la première ligne, et la dernière colonne. 7 doit se trouver à la dernière ligne, première colonne.
Cette case est occupée par 4, on met 7 sous la case courante.
.
Étape 8 : $ \begin{array}{ccccc}
\begin{array}{|c|c|c|}\hline
.&1&6\\\hline 3&5&7\\\hline 4&.&2\\\hline
\end{array}&
\hspace{-0.4cm}\begin{array}{c}
(8)\\\\\\
\end{array}
&\Longrightarrow&
\begin{array}{|c|c|c|}\hline
8&1&6\\\hline 3&5&7\\\hline 4&.&2\\\hline
\end{array}&
\text{ On dépasse la troisième colonne , on met 8 à la première colonne.}
\end{array}$
.
Étape 9 : $ \begin{array}{ccccc}
\begin{array}{ccc}
~&(9)&\end{array}\\
\begin{array}{|c|c|c|}\hline
8&1&6\\\hline 3&5&7\\\hline 4&.&2\\\hline
\end{array}
&\Longrightarrow&
\begin{array}{|c|c|c|}\hline
8&1&6\\\hline 3&5&7\\\hline 4&9&2\\\hline
\end{array}&
\text{ On dépasse la première ligne, on met 9 à la dernière ligne.}
\end{array}$
Le script proposé permettra de générer un carré magique d'ordre impair.
Pour cela vous devez créer trois fonctions :
- la fonction affiche_matrice(matrice) qui permet d'afficher la matrice;
- la fonction matrice_nulle(taille) qui permet de créer une matrice contenant que des zéros à partir de la taille choisie;
- la fonction carre_magique(matrice) qui génère le carré magique. Aide : Algorithme
On donne le programme principal :

4. MOTUS
MOTUS est un jeu où un l'on doit trouver un mot de six lettres en faisant au plus cinq propositions.
Au départ seulement la première lettre est donnée. Pour chaque proposition du candidat on regarde chaque lettre du mot proposé et
on distingue trois cas :
- la lettre se trouve dans le mot cherché et elle est au bon endroit, on la remplace en majuscule dans le mot qui s'affichera;
- la lettre se trouve dans le mot cherché mais pas bien située, on la remplace en minuscule dans le mot qui s'affichera;
- la lettre ne se trouve pas dans le mot cherché on la remplace par un point (.) dans le mot qui s'affichera; .
- la fonction choix_aleatoire_du_mot() qui permet de prendre dans une liste préétablie le mot que le candidat devra trouver ;
- la fonction mot_avec_points(mot) qui génère le premier affichage du mot ne contenant que la première lettre suivi de cinq points
- la fonction mot_construit(mot_choisi, mot_propose) qui crée un nouveau mot , resultat,
en comparant le mot proposé et le mot cherché.
Une méthode :
On transformera la chaîne de caractères mot_choisi en un tableau appelé lettres en utilisant la méthode split() . On écrit lettres = mot_choisi.split('') . Ceci afin de pouvoir modifier une lettre déjà traitées.
On utilisera la méthode indexOf() . En écrivant : position = lettres.indexOf(mot_propose[i]) , position prend la valeur du rang de la lettre mot_propose[i] dans la liste lettres.
Si la lettre mot_propose[i] n'est pas dans la liste lettres alors position prend la valeur -1.
Exemple : mot_choisi = VOLEUR et mot_propose=VIOLON. Ainsi lettres=['V','O','L','E','U','R']
i=0,
mot_propose[i]='V', position = 0. La lettre 'V' du mot proposé est en position 0 dans lettres
i=position donc resultat ='V' et lettres=['0','O','L','E','U','R']. On remplace la lettre trouvé par un '0' pour ne pas avoir à la traiter deux fois.
i=1,
mot_propose[i]='I', position = -1. La lettre 'I' du mot proposé n'est pas dans lettres
donc resultat ='V.' et lettres=['0','O','L','E','U','R'].
i=2,
mot_propose[i]='O', position = 1. La lettre 'O' du mot proposé est en position 1 dans lettres
i $\neq$ position donc resultat ='V.o' et lettres=['0','0','L','E','U','R'].
i=3,
mot_propose[i]='L', position = 2
i $\neq$ position donc resultat ='V.ol' et lettres=['0','0','0','E','U','R'].
i=4,
mot_propose[i]='O', position = -1. La lettre 'O' n'est plus dans lettres
donc resultat ='V.ol.' et lettres=['0','0','0','E','U','R'].
i=5,
mot_propose[i]='N', position = -1.
donc resultat ='V.ol..' et lettres=['0','0','0','E','U','R'].